「数学の概念」を視覚的かつ美しく表現したグラフィックいろいろ

「数学の美しさ」というものは、数学を深く理解することで初めて得られる感覚と言われます。美しさが伝わると数学嫌いも少しはマシになるのかもしれませんが、数学嫌いの人にはそもそも美しさを伝えることができないということで、歯がゆい思いをしている数学愛好家は多いもの。そんなときに便利な、「数学の概念」を視覚的に理解できるグラフィック集は以下の通りです。
soft question - Visually stunning math concepts which are easy to explain - Mathematics Stack Exchange
http://math.stackexchange.com/questions/733754/visually-stunning-math-concepts-which-are-easy-to-explain
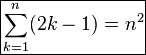
奇数の和が平方数になるのは下の図を見れば一目瞭然。

◆02:偶数の和
偶数の和が n×(n+1) になるのも分かりやすいです。

◆03:展開
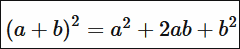
二次方程式の展開は、こんな感じで図示できます。

◆04:多角形の外角の和
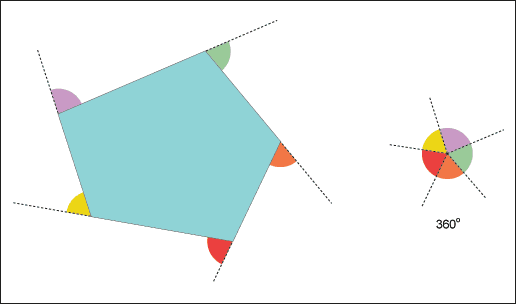
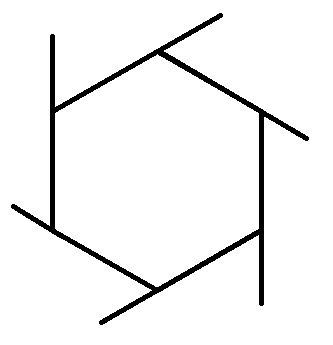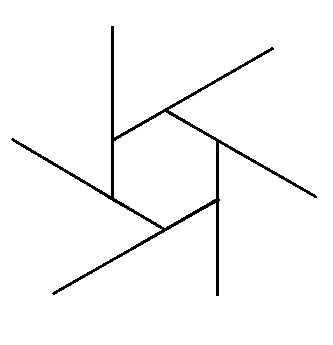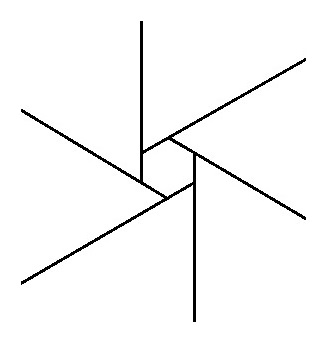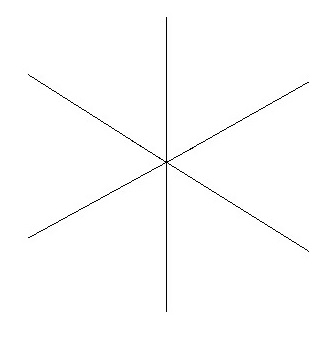
多角形の外角の和が360度というのは、このようなアニメーションなら直感的に理解できます。
◆05:ひし形の面積
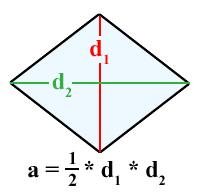
ひし形の面積は、かえって分かりにくくなっている気が……

同じくひし形の面積。こちらはひし形を2つの三角形に分けて考えるもので、どちらかというと視覚的理解というより計算方法のアイデア。
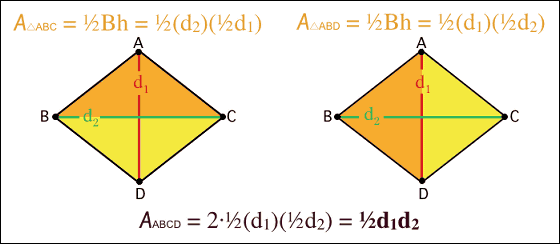
◆06:ピタゴラスの定理(三平方の定理)
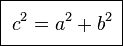
ピタゴラスの定理(三平方の定理)はこんな感じで証明可能。
三平方の定理を円と直角三角形を使って証明したのがこの図。図から得られる関係式を変形すると、ピタゴラスの定理が登場します。

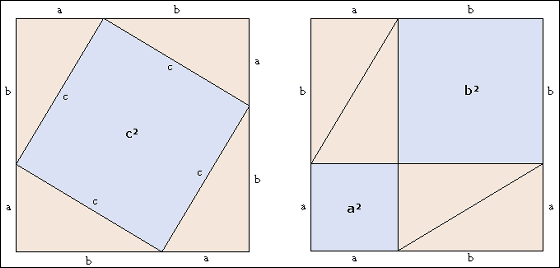
なお、最も一般的な三平方の定理の証明を与える図がこれ。非常にシンプルかつ明快。

三平方の定理の実証実験をするとこんな感じ。
Pythagorean theorem water demo - YouTube
◆07:無限等比級数の和
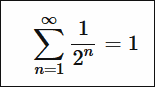
1/2+1/4+1/8+……と無限に足していけば「1」になるのは下の図で表現可能。

1/2+1/4+1/8+……という無限級数の和は、三角形を使って表現することもできます。

◆08:円周率
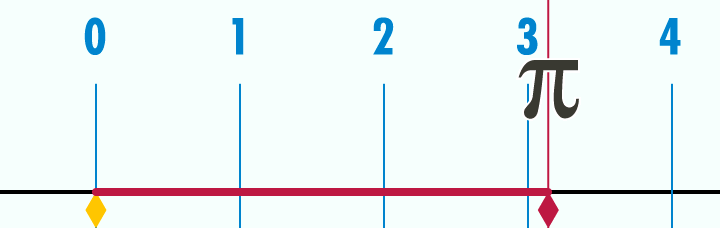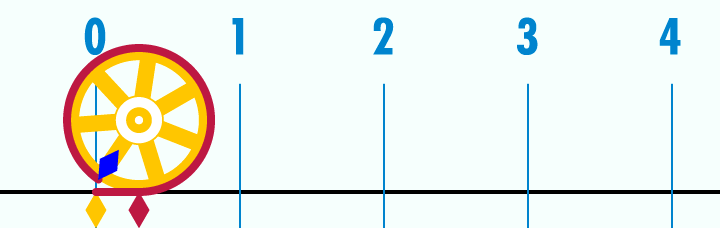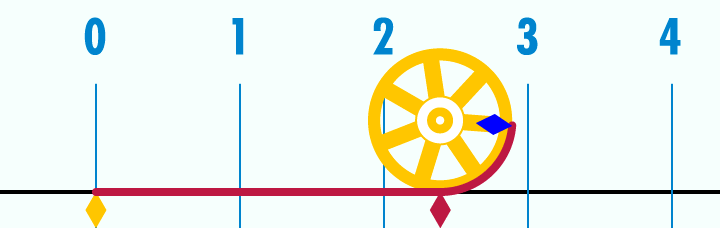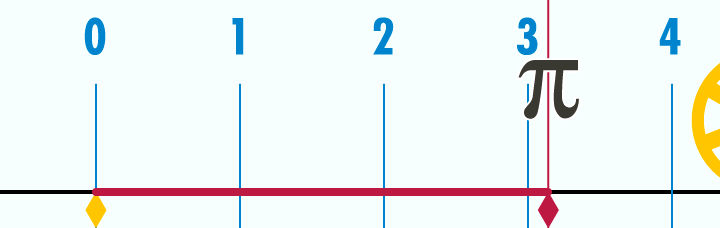
円周率(π)が3.14くらいなのは下のアニメーションを見るとよく分かります。
◆09:円の面積
円の面積がなぜ半径×半径×πなのかはこんな感じ。円をものすごく細かく切って並べ直すと長方形に近づいていきます。

◆10:黄金比
黄金比の描き方。

◆11:sine(サイン)・cosine(コサイン)
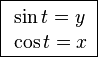
サイン・コサインのグラフがなぜ波形なのか、位相がπ/2rad(ラジアン)違うのかは、下のグラフィックだとよく理解できます。
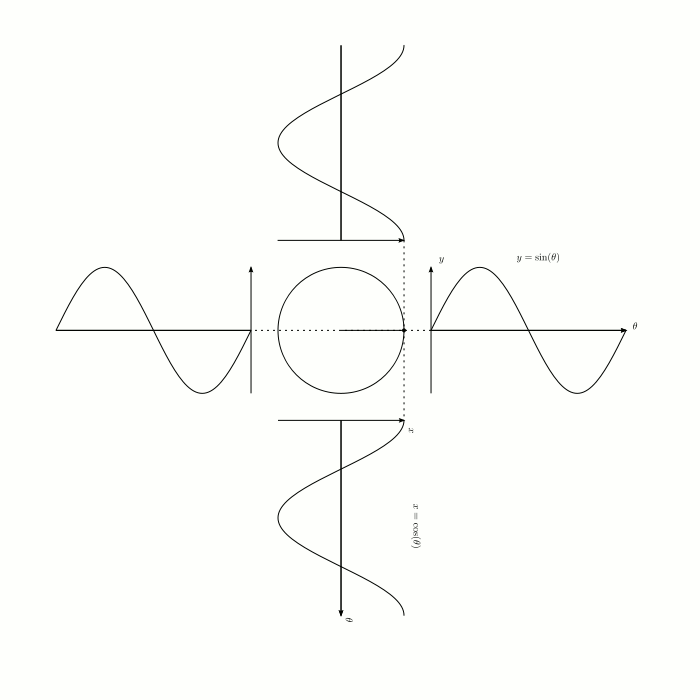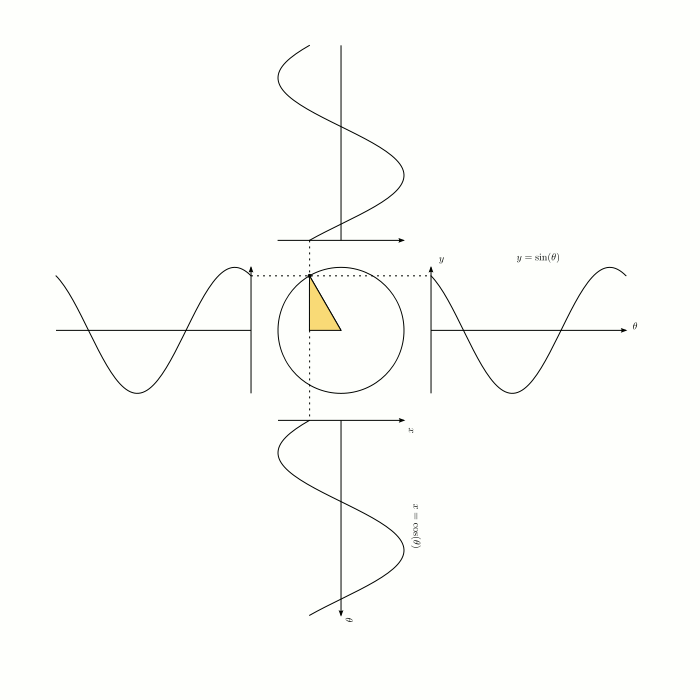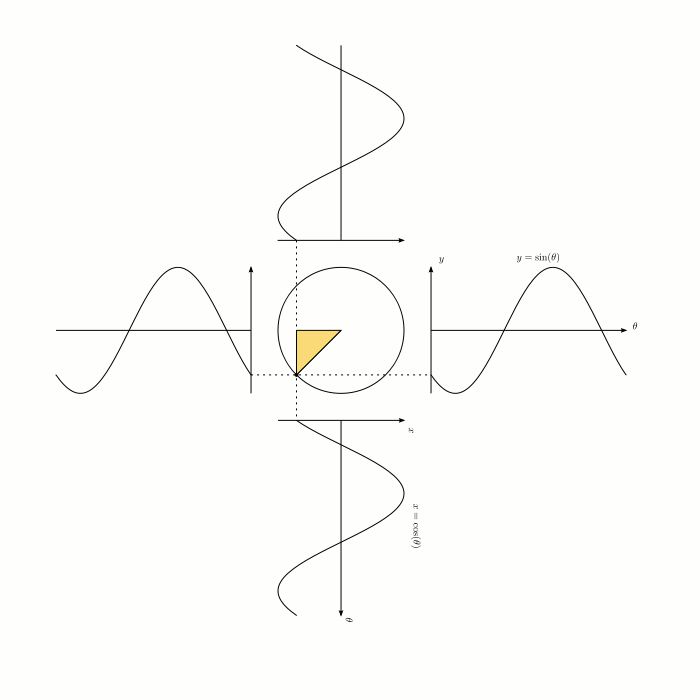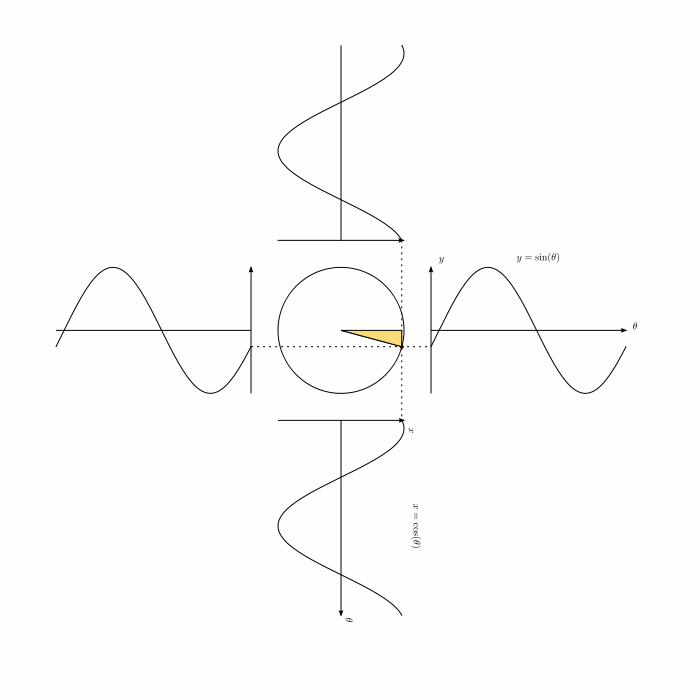
◆12:弧度法
国際単位系の角度を示すラジアンを用いた弧度法の模式図。

◆13:テイラー展開
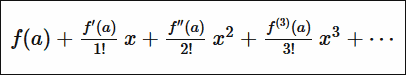
テイラー展開はこんな感じの模式図に。
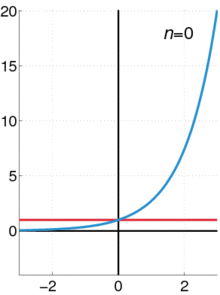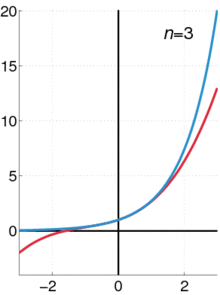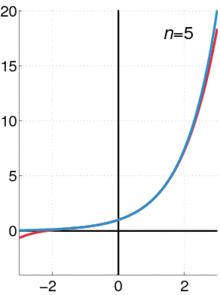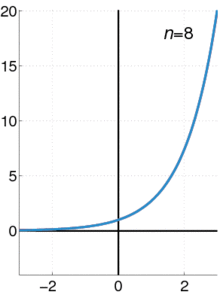
◆14:対数螺旋
対数螺旋を転がした場合の定点の軌跡はこんな感じ。意外なことに原点部分は直線を描くようです。
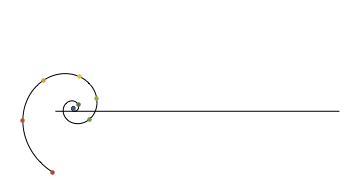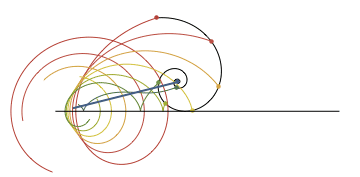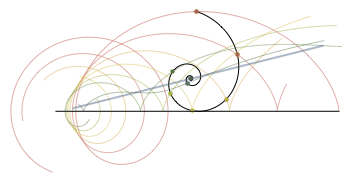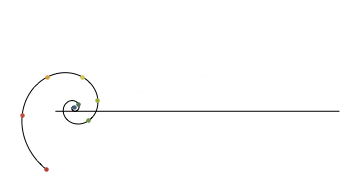
◆15:フーリエ変換
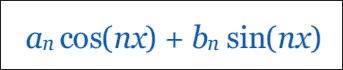
フーリエ変換をビジュアル化するとこんな感じ。
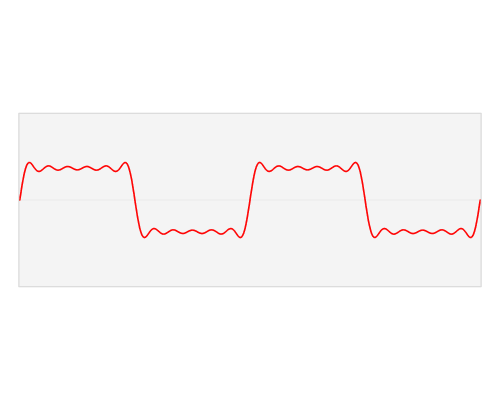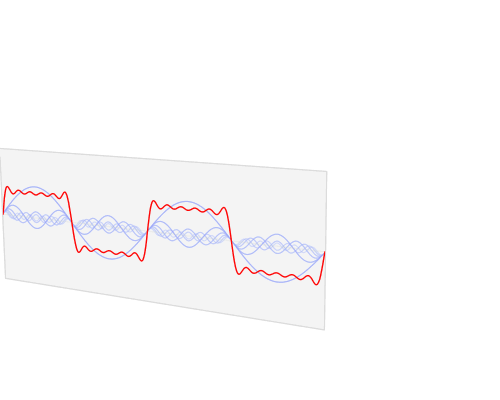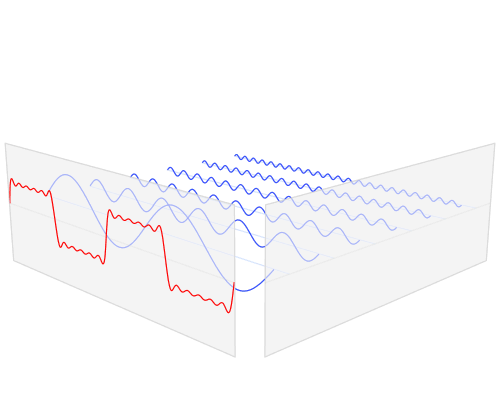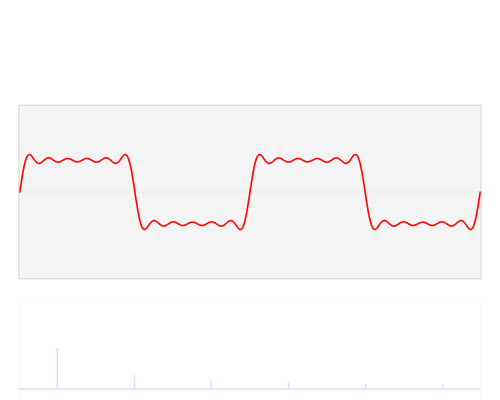
フーリエ変換は下の様に表現することも可能です。
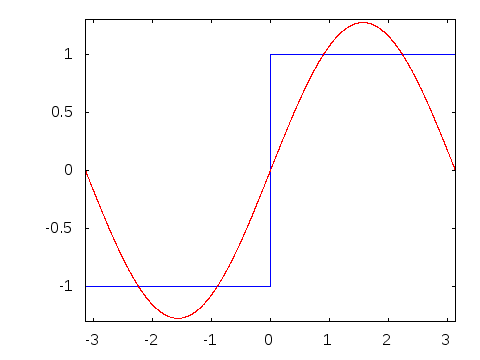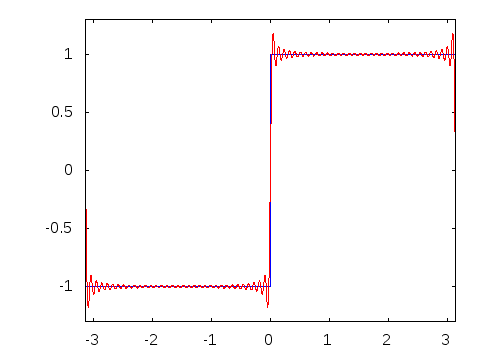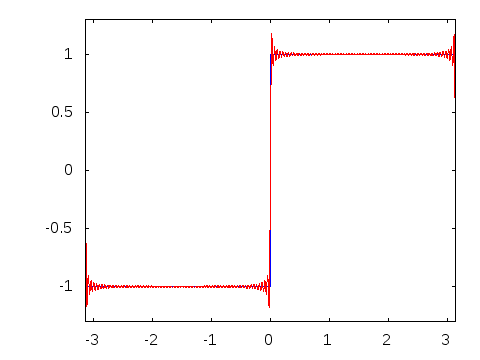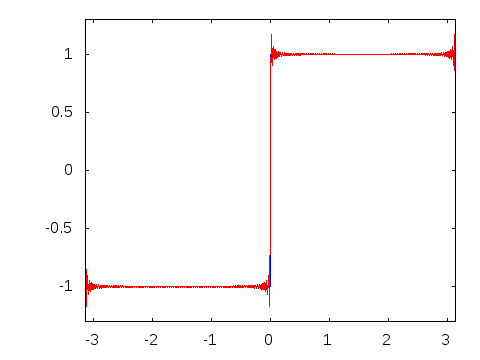
◆16:線積分
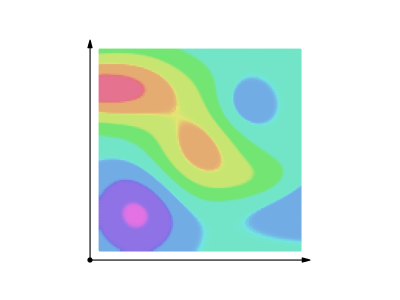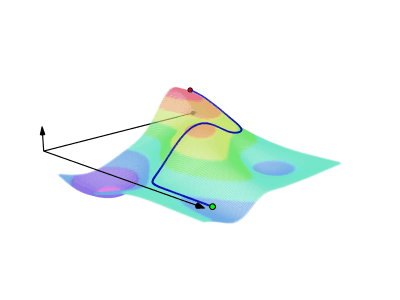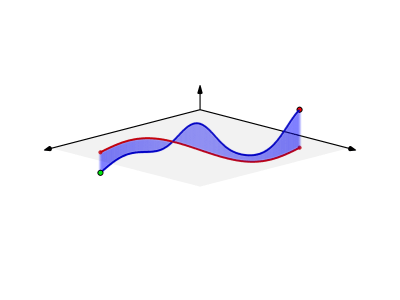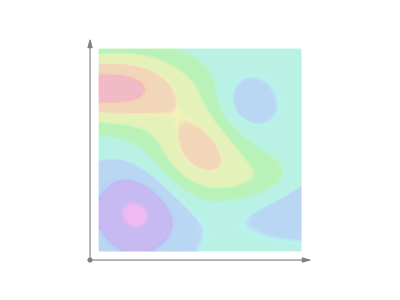
スカラー場の滑らかな曲線に沿った線積分はこんな感じ。
◆17:乗算表
これは乗算表と呼ばれる一定の法則通りに数字を並べた図。1から指定の数(modulo)まで青から赤まで色調を変化させると美しい模様が描かれます。modulo=15はこんな感じ。

modulo=512だとグラデーションがかった模様に。こちらのサイトで模様を作成可能です。

◆18:マンデルブロ集合
マンデルブロ集合を用いたフラクタルデザインの例。

図形の全体と一部分が自己相似になっていると、このような不思議な形になります。

◆19:振り子と磁石
水平面に赤・青・黄色の2つの磁石を正三角形を描くように置き、鉄球のついた振り子を一定のポイントから放つと、3つの磁石はこのような軌跡を描くとのこと。

◆20:おまけ
円周と円の面積をものすごく「粗く」証明するムービーは以下の通りです。
Proof Without Words: The Circle - YouTube








