��������¸�ߤ��뿷���ʷ����֥��եȥ���פ�ȯ������롢���ǤϱԳѤ�2�Ļ����������ǤϱԳѤ�����ʤ�����

�֥��ڥ��ȹ��ʷк���ؤȥ��å����ե�������ؤθ�������ब��������¸�ߤ��뿷���ʷ������饹����Soft cells(���եȥ���)�פ�ȯ�����ޤ��������եȥ���ϡ֥��ޥͥ������̡סֶ����ݡס֥����६���γ̤���¦�פʤ�¿�ͤʾ���¸�ߤ��Ƥ��ꡢ�������֤ǤϱԳѤ�2�Ļ��������������֤ǤϱԳѤ�����ʤ��פȤ�����ħ�������Ƥ��ޤ���
Soft cells and the geometry of seashells | PNAS Nexus | Oxford Academic
What Do Onion Skins and Zebra Strips Have in Common? New Geometric Shapes Identified by BME Mathematicians | BME central site
https://www.bme.hu/en/news/240910/bme-epk-research-soft-cells-discovery-publication
Mathematicians discover new universal class of shapes to explain complex biological forms | University of Oxford
https://www.ox.ac.uk/news/2024-09-12-mathematicians-discover-new-universal-class-shapes-explain-complex-biological-forms
���ؤ�ʬ���1�Ĥˡ��ֶ��֤��֤ʤ�������פˤĤ��Ƹ��椹��ʬ�����ޤ�������ʬ��Ǥϰ���Ū�˻��ѷ���¿�ѷ��Ȥ��ä���ľ����ʣ���αԳѤǹ������줿���פ������оݤȤʤ�ΤǤ����������η����ϼ������ǤϤ��ޤ긫���ޤ���
���������ϡ���������ʪ�Τ��������Ƥ����ľ����ԳѤΤʤ������פ����Ū������������ˡ���ɵڡ����η�̡��֥��եȥ���פȸƤФ�뿷���ʿ���Ū�����ˤ�äƼ�������¿����ʪ�Τ�����Ω�äƤ��뤳�Ȥ��ͤ��ߤ�ޤ�����
���եȥ���ϡ������֤Ǥϡ�2�ĤγѤȶ����ǹ������줿���פȤ���ɽ������ޤ������եȥ���ˤ�äƹ�������륿���빽¤����ϰʲ����̤ꡣ���ʤ��ֻ��ѷ��˻������եȥ���ס����ʤ��ֻͳѷ��˻������եȥ���ס����ʤ���ϻ�ѷ��˻������եȥ���פΥ����빽¤�Ǥ���

���եȥ��뤬�������Ǹ�����㤬�ʲ����ֲ���ס֥��ޥ��ޤΤ������͡סֳ������̡ס��������ü�δ����إ�ǥ�סֶ����ݡס֥��ޥͥ������̡ס־����סַ������̡פʤɤ˥��եȥ��뤬�ѻ�����ޤ����ޤ�����ü��������Ȥʤä�����Ω������ǥ�����Ƥκ�ԤǤ�����۲ȤΥ��ϡ��ϥǥ��ɻ�Υǥ�����ˤ⥽�եȥ��뤬����뤳�Ȥ��Ƥ��ޤ���
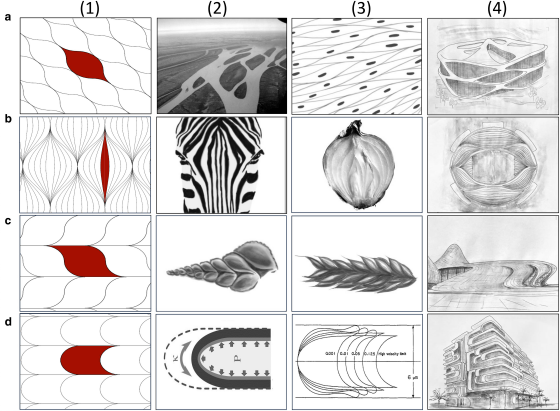
���������֤Ǥϥ��եȥ���ϡֱԳѤ�1�Ĥ�����ʤ������פȤ��Ƹ���ޤ������������ϻ��������֤ˤ����륽�եȥ������Ȥ��ƥ����६���γ̤����Ƥ��ޤ���

���������ΰ���Ǥ��륬�ܡ��롦�ɥ⥳���嶵���ϡ�¿���ξ�硢�����ʴ�����Ū��¤�α��Ѳ�ǽ����ȯ������Ĺ��ǯ��������餫�ˤʤ�ޤ������եȥ���˴ؤ��ƤϿ���Ū���ꡦ��ʪ��Ū���ꡦ���۳�Ū����˱��ѤǤ��뤳�Ȥ����Ǥ����餫�ˤʤäƤ��ޤ�����������¾��ʬ��Ǥ�ʳ�Ū��ͭ�ѤǤ��뤳�Ȥ���������ǽ��������ޤ��פȽҤ٤Ƥ��ޤ����ޤ���Ʊ�������������ΰ���Ǥ��륢�饤���ꥨ������ϡּ����Ͽ�������������Ǥʤ����ԳѤ�����褦�Ǥ��פȥ����Ȥ��Ƥ��ޤ���








