アインシュタインのノートには何が書かれているのか?

By Sebastian Niedlich
アルベルト・アインシュタインといえば、一般相対性理論を含むさまざまな理論を提唱した理論物理学者で、「天才」という言葉の代名詞のような人物です。そんなアインシュタインの思考の一端が垣間見える、貴重なプライベートでの推論や計算が書き込まれたノート「チューリッヒ・ノート」の中身が公開されています。
Einstein's Zurich Notebook
http://www.pitt.edu/~jdnorton/Goodies/Zurich_Notebook/index.html
◆ノートの表紙
ノートには2つのカバーがあります。アインシュタインはこの両方に説明書きを行っており、以下のカバーにはアインシュタインの秘書であったヘレン・デュカスがタイプライターで打った「Notes for Lectures on Relativity…(相対性理論を説明するためのノート)」という文字。

そしてこのノートをひっくり返すと、「Relativity(相対性理論)」とアインシュタイン本人の手で書かれたもうひとつのカバーが見つかります。

そして、「Relativity」と書かれたカバーの内側には、以下のようなラフスケッチがあります。これらは、全て数学パズルです。
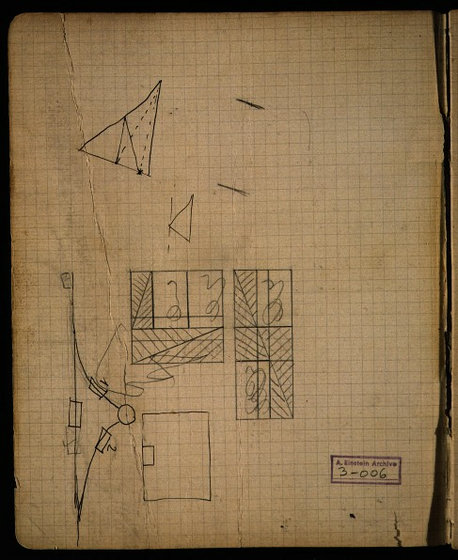
以下の図はレール上を走る鉄道車両と分岐路に関する問題で、線がレール、長方形が鉄道車両を表しています。
複数の正方形や長方形が並んでいる以下の図は、一辺の長さが「8」の正方形を、長辺「13」短辺「5」の長方形に組み替える、という数学パズル。一辺の長さが「8」の正方形は、面積が「8×8=64」になります。
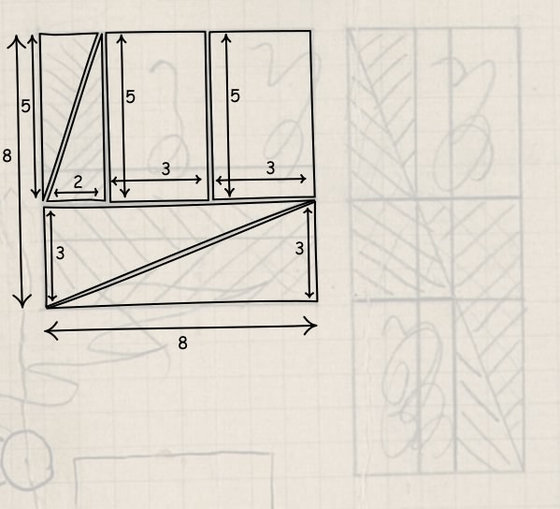
しかし、正方形を細かく分割して組み替えることで完成する長方形の面積は、「13×5=65」になっており、なぜか面積が増えています。もちろんアインシュタインはこのパズルが「なぜ面積が増えるのか?」をしっかりと理解しているはずですが、真に謎なのはアインシュタインがなぜこのような数学パズルで遊んでいたのか、というところ。ノートを1枚1枚解説しているピッツバーグ大学のジョン・D・ノートン氏は「もしかすると誰かの子どもと遊んでいたのかも」と記述しています。
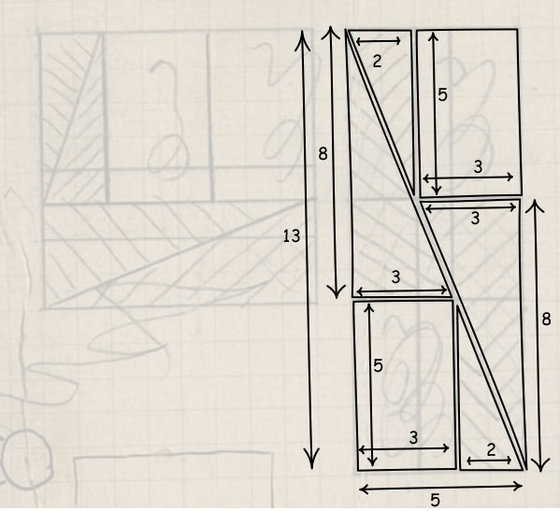
なお、正方形を長方形に組み替えると面積が大きくなってしまう謎の答えは、ここから確認できます。
◆四次元電気力学
このページでは相対性理論やミンコフスキーの電気力学に対する元素の四次元アプローチについて詳しく述べています。
四次元空間を(x、y、z、ict)=(x1、x2、x3、x4)とし、スカラー量から4元ベクトルや6元ベクトル、その演算方を解説しています。

◆初めての一般相対性理論の線素
電気力学と熱物理学の概念について詳しく述べているページが13ページほど続き……
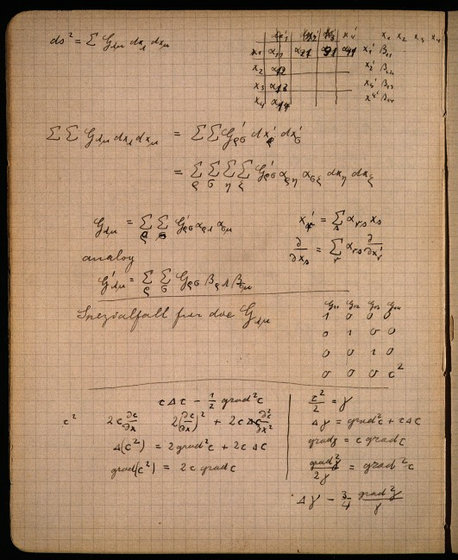
そして突然何の前触れもなく、一般相対性理論の基本概念である「線素」が紙の1番上に書かれています。これについてノートン氏は「これはアインシュタインが初めて線素を書き記した際のものかもしれない」と述べています。
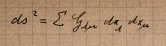
上記の式中にある「Gμν」という記号は、計量テンソル。ノートの中でも何度か登場するこの係数は、何度かアインシュタインの手で書かれる内に小文字の「g」で表現するように変化していっています。なお、計量テンソルは「重力の逆二乗則」を基にした「重力場方式」であるそうです。

なお、アインシュタインが「線素」についての考えを巡らしたであろうこれらのページでは、テンソル解析(PDFファイル)などの解析方法は使用していません。

◆曲面上の運動
曲面上の運動に関する分析は、3ページに渡って続けられています。
これらのページ上では、アインシュタインが古典物理学からいくつかの重要な概念を発見しています。もし、ある物体が慣性に従って曲面上を動くなら、曲面上を動く物体の軌道は、曲面上の2点を結ぶ最短距離を示す測地線になります。

曲面はスカラー場「f」により定義され、曲面上を動く物体は運動方程式により、加速度ベクトル(d2x/dt2、d2y/dt2、d2z/dt2)として表せます。さらに、曲面の反力と比例しているので、「f」の傾きから(∂f/∂x、∂f/∂y、∂f/∂z)と表せるようになり、式は以下のように簡略化可能。
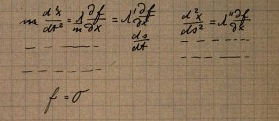
◆その他
他にも熱物理学の熱放射に関する統計や……

一般相対性理論の万有引力についてのメモ

計量テンソルに関する考察など、さまざまな計算式が書き記されています。

数式の内容についてはほとんどチンプンカンプンでも、プライベートなノートの中身がこれだけ数式でびっしりであることを見せつけられれば、アインシュタインがいかに物理学の理論を導き出すために心血を注いでいたかは想像できます。








